La lettre « p » : petite par la taille mais grande par l’esprit

Comprendre la science des données

• Centre de Compétence Méthodologie & Statistiques (CCMS)

Cet article a été publié dans MedinLux et fait partie d’un effort de collaboration visant à rendre les concepts statistiques et épidémiologiques accessibles aux professionnels de la santé au Luxembourg.

Cet article est le premier d’une série sur des questions de méthodologie statistique, permettant de fournir les outils afin de mieux comprendre et d’interpréter les articles scientifiques. L’objectif est d’acquérir un esprit critique et de connaître les bonnes pratiques à suivre lors de la lecture de publications d’informations scientifiques (ou lors de l’analyse de vos données). Dans la recherche biomédicale, il est commun de lire « statistiquement différent », ou « significativement plus grand/petit », de voir des tableaux avec une colonne où la lettre « p » apparaît, ou bien encore des graphiques contenant des étoiles (ou d’autres symboles). Tout ceci fait référence à la même idée: la valeur-p, ou p-valeur (probability value en anglais). Mais à quoi correspond-t-elle? Dans cet article, nous allons vous la présenter plus en détails.

UN EXEMPLE DE LA LITTERATURE, AFIN D’ILLUSTRER NOTRE PROPOS

Dans un article scientifique datant de 2021, les auteurs ont étudié le poids à la naissance de bébés selon la consommation de tabac des mères (1), en tenant compte de l’indice de masse corporelle (IMC) de ces dernières. Les données étaient issues d’une enquête allemande périnatale et concernaient plus de 110.000 grossesses, suivies entre 2010 et 2017. Le résumé indiquait que les différences de poids des bébés entre les fumeuses et les non-fumeuses étaient toujours statistiquement significatives (p < 0,001), quel que soit l’IMC de la mère.

Faisons l’exercice de se mettre dans la peau de l’équipe qui a mené la recherche et de se poser les questions qui ont dû être les leurs. L’objectif de l’équipe était d’analyser la relation entre le tabagisme et l’effet du poids de naissance, en tenant compte de l’IMC maternel. La figure 1 montre les différentes étapes depuis la définition de l’hypothèse de recherche jusqu’aux conclusions.

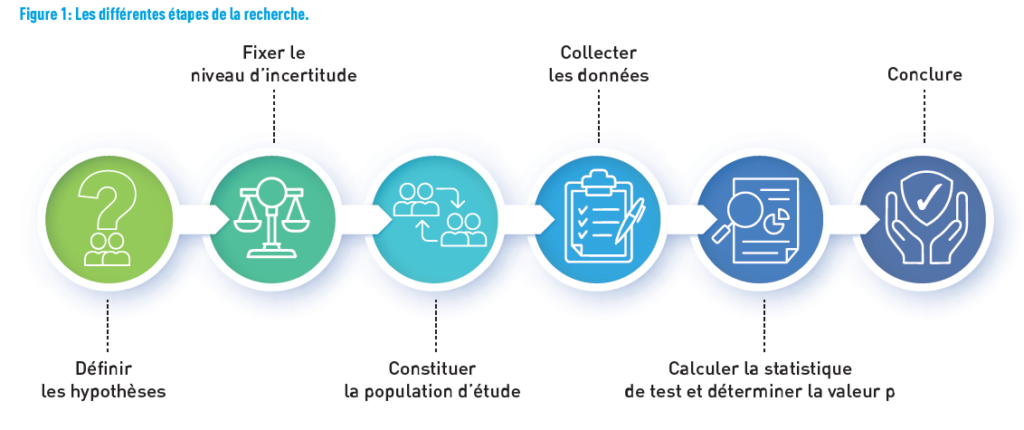
D’ABORD, DEFINIR L’HYPOTHESE

En recherche, la démarche hypothético-déductive vise à définir une hypothèse nulle et une hypothèse alternative de manière explicite. L’hypothèse nulle est formulée dans le but d’être rejetée. Elle est considérée comme vraie tant que le contraire n’a pas été démontré. À l’inverse, l’hypothèse alternative est celle que l’on cherche à montrer. Elles sont disjointes: elles ne peuvent pas se réaliser toutes les deux en même temps.

Dans notre exemple, l’hypothèse nulle est «il n’y a pas de différence de poids entre les bébés, que la mère fume ou non», tandis que l’hypothèse alternative peut s’énoncer ainsi: «une différence de poids de naissance des bébés existe entre les fumeuses et les non-fumeuses».

En pratique, la décision se base sur l’hypothèse nulle, sachant que l’on souhaite prouver l’hypothèse alternative. Ainsi, les scientifiques utilisent des tests statistiques pour déterminer si l’hypothèse nulle est vraie ou fausse. S’ils peuvent démontrer avec une certaine probabilité que l’hypothèse nulle est fausse, alors l’hypothèse alternative sera acceptée (2).

FIXER LE NIVEAU D’INCERTITUDE

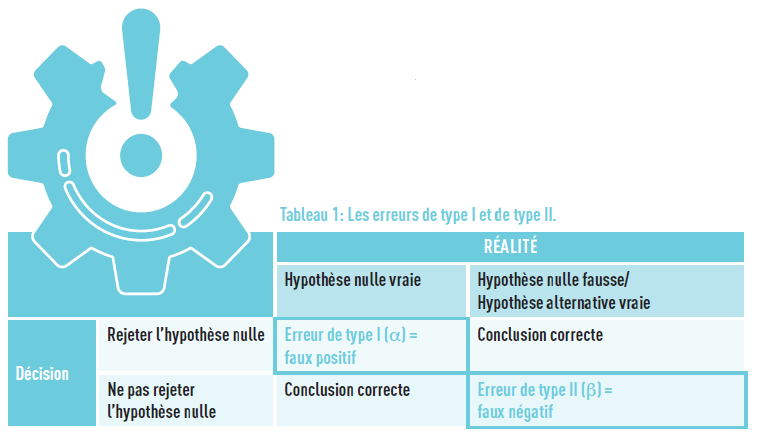
Une fois que les hypothèses sont clairement énoncées, on va s’intéresser au niveau d’incertitude, c’est-à-dire le niveau de risque d’erreur que l’on accepte en rejetant l’hypothèse nulle (et ainsi accepter l’hypothèse alternative), alors qu’elle est vraie. Il s’agit du risque de première espèce, ou de type I, noté α. Il est à déterminer selon les domaines et les enjeux de l’étude. En général, il est fixé à 5% (de façon bilatérale, i.e. il existe une différence
dans un sens ou l’autre). Cela signifie que si l’étude est réalisée 100 fois (sur des échantillons différents par exemple), l’hypothèse nulle sera rejetée 5 fois alors qu’elle était vraie.

REMARQUE DE LA STATISTICIENNE
La valeur de 5% n’est pas choisie au hasard. Cette limite est issue d’une distribution normale (encore appelée Laplace-Gauss, c’est la fameuse courbe en cloche; référence absolue chez les statisticiens, elle correspond à la distribution de nombreuses variables biologiques): lorsque les valeurs sont éloignées de plus de deux écarts-types (dans le cas d’une distribution normale avec une erreur de première espèce de 5%, seuil de 1,96) par rapport à la moyenne, elles sont considérées comme inhabituelles (3). Le statisticien peut chercher à minimiser ce risque en choisissant par exemple un seuil de 1% au lieu de 5%, avec pour conséquence qu’il sera plus difficile de rejeter l’hypothèse nulle.

Une autre erreur à prendre en compte est celle du «faux positif». Lors du test d’hypothèse statistique, il se peut que l’on accepte l’hypothèse nulle alors qu’elle est fausse, c’est ce qu’on appelle l’erreur de type 2, notée β. Dans notre exemple, cela correspondrait à dire que les bébés ont le même poids, peu importe si leur mère fume ou non (alors que ce n’est pas le cas). Cette erreur est utilisée dans le calcul de la puissance du test (1- β), qui
se traduit par la probabilité de rejeter l’hypothèse nulle sachant qu’elle est fausse.

Ces deux erreurs sont liées: quand l’une est diminuée, l’autre va augmenter et vice-versa. Le tableau 1 résume les situations.

CONSTITUER LA POPULATION DE L’ETUDE

Avant de se lancer dans une étude, il est important de déterminer le nombre de participants à inclure. Pourquoi effectuer cette démarche? C’est pour éviter de recruter trop de patients, ce qui engendrerait des coûts importants et/ou de temps, ou qui poserait un problème éthique dans le cas d’études interventionnelles (exposition à des traitements potentiellement inefficaces, voire dangereux). A contrario, un échantillon de taille trop réduite ne permettrait pas d’obtenir une puissance suffisante (et ne permettrait pas d’obtenir une conclusion).

Plusieurs informations sont nécessaires pour déterminer ce nombre: la taille de l’effet ciblé (en se basant sur des recherches déjà existantes entre autres), la puissance, l’erreur de type I, la variance des données, mais aussi le modèle statistique utilisé lors de l’analyse.
L’échantillon doit en outre être représentatif de la population cible à étudier, c’est à dire partager avec cette dernière une série de propriétés importantes. Ainsi, l’échantillon représente de la manière la plus fidèle les caractéristiques de la population cible, par exemple la même
proportion de femmes/hommes, l’âge moyen… Sans cela, les résultats obtenus dans l’étude ne peuvent pas être généralisés.

Dans l’exemple choisi, les auteurs ont cherché des données sur les bébés et sur le statut tabagique des mères.

COLLECTER LES DONNEES

Une fois que tout cela a été fixé (donc en amont), les données peuvent être recueillies.

Dans notre exemple, les chercheurs ont utilisé une importante base de données (province de Schleswig-Holstein), qui rentrait dans le cadre du German Perinatal Survey et comprenait 110.047 grossesses uniques enregistrées entre 2010 et 2017. C’est donc une étude de registre (nous reviendrons ultérieurement sur les différents types d’études, avec leurs avantages, leurs inconvénients et leurs limitations), avec un effectif considérable (ce qui
est un gage de puissance, voir encadré).

Au terme de la collecte des données, on pourra calculer les différents indicateurs prévus dans le protocole qui permettent de répondre à la question de recherche (comme par exemple la moyenne sur un paramètre dans les différents groupes, un odds ratio, un risque relatif…). Ces différentes notions seront vues dans un prochain article. Pour revenir à notre exemple, les chercheurs ont calculé le poids moyen des bébés dans le groupe des fumeuses et le poids moyen dans le groupe des non-fumeuses, et ils ont comparé ces deux chiffres, en tenant compte
de l’IMC de la mère pendant la grossesse.

CALCULER LA STATISTIQUE DE TEST ET DETERMINER LA VALEUR P

La question fondamentale qui se pose à ce stade est de savoir si la différence que l’on constate au niveau de notre indicateur – le poids de naissance des bébés en fonction du statut tabagique de la mère – est lié à ce dernier ou à un effet du hasard. Pour y répondre, on a recours à des tests statistiques, comme le test des moyennes ou des médianes, ou encore le test du Chi-carré pour ne citer que les plus connus et qui donneront cette fameuse valeur p. Toutefois, un statisticien sera toujours de très bon conseil pour vous indiquer quel test est le plus approprié à utiliser dans votre recherche.

La valeur p est une probabilité et est donc comprise entre 0 et 1. Plus la valeur p est petite, plus les preuves contre l’hypothèse nulle sont importantes. Elle sera ensuite comparée à l’erreur α, définie précédemment. Si la valeur p est plus petite que l’erreur α, alors les résultats sont statistiquement significatifs, l’hypothèse nulle est rejetée avec un risque de α. À l’inverse, si la valeur p est plus grande, l’hypothèse nulle est acceptée.

REMARQUE DE LA STATISTICIENNE
Pour de bonnes pratiques, il est fortement conseillé d’indiquer la valeur de p, au lieu de présenter une étoile (ou autre symbole) dans un graphique, ou de mettre «< 0,05» dans un texte ou un tableau!

Dans notre exemple, le poids de naissance était le plus élevé chez les non-fumeuses. Dans tous les groupes d’IMC maternel, le poids de naissance diminuait significativement avec le nombre de cigarettes fumées par jour (p < 0,001). Autrement dit, le hasard a moins de 1 chance sur 1.000 d’expliquer les différences observées.

L’INTERVALLE DE CONFIANCE: UN AUTRE INDICATEUR, AVEC DE NOMBREUX AVANTAGES

L’intervalle de confiance (IC) permet d’avoir plus d’information que la valeur p: il présente l’amplitude à 95% de l’effet mesuré (correspondant à un risque de 5%). Cela signifie que si nous faisons l’estimation de l’effet 100 fois (dans d’autres conditions: personnes différentes, région différente, temporalité différente…), le résultat serait compris dans l’intervalle 95 fois sur les 100 expériences. De plus, en se basant sur l’IC, les conclusions sur la significativité statistique peuvent aussi être établies: en reprenant l’exemple introductif, si l’odds ratio (surplus de «malchance»; l’odds ratio sera présenté plus en détails lors d’un prochain article) est calculé entre le fait d’avoir un bébé né prématurément ou non selon le statut tabagique de la mère, et que la valeur 1 n’est pas contenue dans l’intervalle, cela signifie qu’un effet statistiquement significatif est notable entre ces deux variables au
risque de 5%. Un avantage non négligeable qu’apporte l’IC est la variabilité de la mesure. En effet, s’il est large, l’estimation est moins précise que dans le cas où il est plus restreint.

REMARQUE DE LA BIOSTATISTICIENNE: FAUX POSITIF ET NÉCESSITÉ DE CORRECTION DES TESTS MULTIPLES

Une complication peut apparaître avec la valeur p dans le cas où plusieurs tests sont effectués sur le même échantillon. Reprenons l’exemple de l’étude de l’effet du tabac sur le poids des bébés et imaginons que les auteurs souhaiteraient aussi tester l’effet de la prise de certains médicaments, de l’activité physique (douce, modérée ou forte), de la consommation de fruits et de légumes, du fait de faire des travaux de rénovation dans la maison (pour préparer l’arrivée du bébé) ou du stress pendant la grossesse. Par définition, 5 études menées sur 100, avec un niveau de 5% pour chacune d’entre elles, auront un résultat faussement positif.

Pour tenir compte de l’inflation de l’erreur de première espèce – conclure à tort qu’il y a une différence – lors de la multiplicité des tests, des solutions existent, telle que la correction de Bonferroni (la plus connue). Un statisticien sera une fois de plus le meilleur interlocuteur pour vous proposer la solution à ce problème!

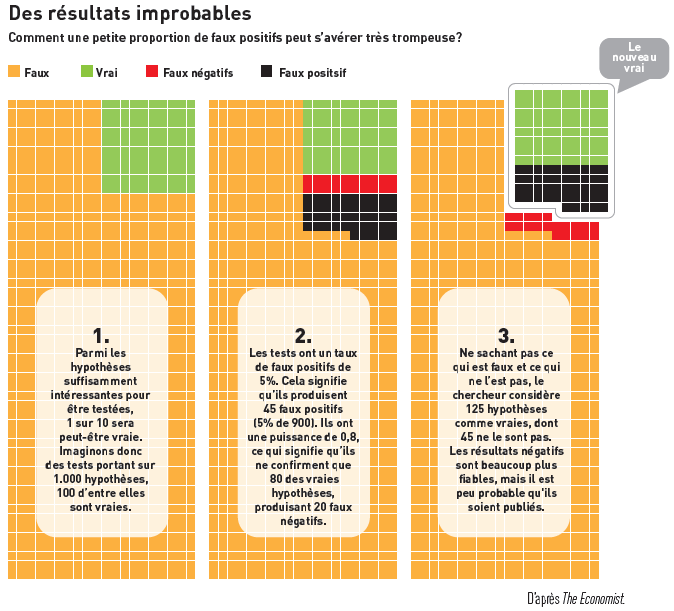
Pour faire un parallèle avec la justice, l’erreur de type I correspond à juger quelqu’un de coupable alors qu’aucun crime n’a été commis, et l’erreur de type II est de juger la personne comme innocente, alors qu’elle a commis le crime

REMARQUE DE LA STATISTICIENNE : LE TRITURAGE DES DONNÉES

Certains chercheurs prennent les choses à l’envers, même si cela n’est pas fait de façon volontaire. Plutôt que de tester une hypothèse et subissant probablement une pression pour publier, ils vont à la pêche aux associations statistiques. Plusieurs noms existent pour désigner cette pratique: p-hacking, data dredging, data fishing, data snooping ou data butchery. Cela peut se présenter sous plusieurs formes: faire des analyses jusqu’à trouver des résultats avec une valeur p sous un certain seuil (généralement 0,05), changer le critère d’évaluation, utiliser un jeu de données restreint avec une population différente de celle d’origine (en excluant des participants ou en ne prenant qu’une catégorie particulière de la population, par exemple), en utilisant plusieurs/d’autres variables d’ajustement (ou en oublier), ne montrer que les tests significatifs (biais de publication). Ainsi, en enlevant les tests non significatifs, la probabilité de trouver des résultats significatifs augmente. La non-utilisation de correction des tests multiples est une façon de modifier les résultats, du fait que des résultats soient significatifs par pur hasard (cf. paragraphe précédent).

De plus en plus de journaux sont sensibilisés à ces problème: c’est pourquoi ils demandent la publication des données, afin de pouvoir répliquer les analyses et de retrouver les résultats publiés.

La bonne pratique est d’écrire en amont un plan d’analyse statistique, en décrivant les différentes analyses, avec les hypothèses, et les solutions envisagées avec toujours le soutien d’un statisticien.

CONTROVERSE DE LA VALEUR P

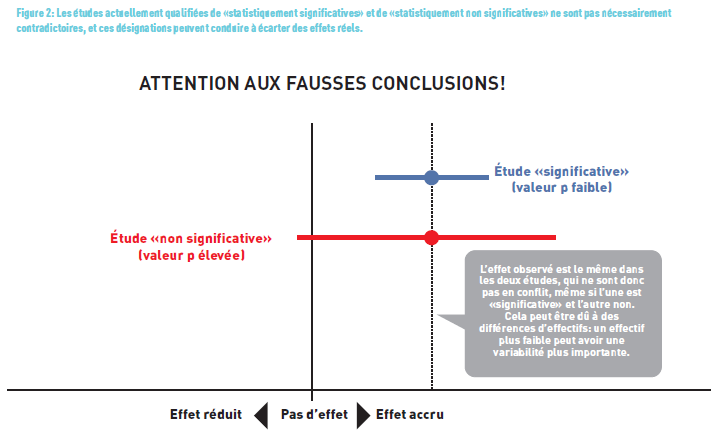
Ces dernières années (voire décennies), de nombreux statisticiens ont décrié cette valeur p, notamment dans un article publié dans Nature (4) (Figure 2). Dans ce dernier, les auteurs ont relevé notamment que 51% des 791 articles parmi 5 journaux ont eu une mauvaise interprétation de la valeur p. Ils souhaiteraient que cet indicateur ne soit plus dichotomisé en «statistiquement significatif»/«statistiquement non significatif» pour prendre une décision. La valeur de «p» ne doit pas être jugée ex abstracto, mais replacée dans son contexte, en se rappelant bien que la signification statistique est différente de la signification clinique.

TAKE HOME MESSAGE

La valeur p – plus communément appelée «petit p» – est un standard dans les articles scientifiques, même si son interprétation peut être erronée. Toutefois, en appliquant certaines règles, il est possible d’éviter les pièges évoqués lors de cet article ou même de donner une meilleure vision des estimations en utilisant des intervalles de confiance. La détermination du calcul de la valeur de «p» est technique, car elle nécessite des connaissances et des compétences pour déterminer le test statistique approprié. Souvent, le seuil de significativité est fixé à 5% (0,05), mais il peut être abaissé afin de diminuer (ou d’accroître respectivement) la probabilité que les différences observées soient liées au hasard. En outre, on ne devrait pas voir son interprétation de façon binaire (significatif/non significatif) comme le bon/le mauvais, mais savoir qu’il est important de tenir compte de l’ensemble de l’étude et plus particulièrement de l’effet mesuré! N’hésitez pas à nous faire parvenir vos questions sur des thématiques épidémiologiques ou statistiques particulières. Nous y répondrons ultérieurement.

«NON SIGNIFICATIF» NE SIGNIFIE PAS «PAS D’EFFET»!
Une étude peut ne pas montrer d’effet en raison d’un nombre de participants/échantillons insuffisant (qui affaiblit la puissance de l’étude, c’est-à-dire sa capacité à rejeter l’hypothèse nulle alors que cette dernière est fausse), voire d’une erreur de type 1 (faux positif). Il est important de distinguer la significativité statistique – qui atteste avec un certain degré d’incertitude de la réalité d’une différence – de la pertinence clinique de cette différence. Pour écrire ce postulat, la mesure à prendre en compte est la taille (ou force) de l’effet, par exemple par le biais d’un risque relatif important. Nous reviendrons ultérieurement sur cette notion fondamentale.

Dans le même ordre d’idées, un résultat statistiquement significatif ne permet pas de présumer d’un éventuel lien de causalité. Ainsi, dans un travail publié dans le New England Journal of Medicine (5), les auteurs avaient trouvé une corrélation fortement significative (r = 0,791 et p < 0,0001) entre la consommation de chocolat et le développement des fonctions cognitives, mesuré par le nombre de prix Nobel par pays. Ils ont conclu, non sans humour, qu’il reste à déterminer si la consommation de chocolat est le mécanisme sous-jacent de l’association observée avec l’amélioration des fonctions cognitives. Nous verrons ultérieurement que pour établir un lien de causalité entre un facteur et un événement, un certain nombre de critères (dits de «Bradford et Hill») doivent être rencontrés.

Le résumé des notions statistiques, par la biostatisticienne

• Le but d’un test statistique est de tester une hypothèse nulle (notée H0).
• L’hypothèse nulle concerne un paramètre de la population
• L’hypothèse nulle est celle que l’on veut rejeter. Elle exprime souvent l’absence d’effet. Par exemple: l’effet du traitement A est le même que l’effet du traitement B.
• L’hypothèse alternative (notée H1) est celle que l’on aimerait accepter. Par exemple: l’effet du traitement A est différent de l’effet du traitement B.
• On distingue 2 types d’erreurs:
  • l’erreur de type I: rejeter H0 alors qu’elle est vraie (faux positif). La probabilité de commettre cette erreur est égale à α;
  • l’erreur de type II: ne pas rejeter H0 alors qu’elle est fausse, c’est-à-dire quand H1) est vraie (faux négatif). La probabilité de commettre cette erreur est égale à β.
• La puissance d’un test statistique est égale à 1-β. C’est la probabilité de rejeter H0 quand elle est fausse (et donc que H1 est vraie).
• Les tests statistiques permettent de déterminer la valeur p, qui est une probabilité (donc comprise entre 0 et 1).
• Plus la valeur p est petite, plus les preuves contre l’hypothèse nulle H0 sont importantes. Si la valeur p est plus petite que l’erreur α, alors les résultats sont statistiquement significatifs. À l’inverse, si elle est plus grande, l’hypothèse nulle est acceptée.

References

1. Günther V, Alkatout I, Vollmer C, et al. Impact of nicotine and maternal BMI on fetal birth weight. BMC Pregnancy Childbirth 2021;21:127. https://doi.org/10.1186/s12884-021-03593-z
2. www.eupati.eu
3. Cowles, M., & Davis, C. (1992). On the origins of the .05 level of statistical significance. In A. E. Kazdin (Ed.), Methodological issues & strategies in clinical research (pp. 285–294). American Psychological Association. https://doi.org/10.1037/10109-026
4. Amrhein, Valentin, Sander Greenland, and Blake McShane. 2019. “Scientists Rise up against Statistical Significance.” Nature (London) 567 (7748): 305–7. https://doi.org/10.1038/d41586-019-00857-9.
5. Messerli FH. Chocolate Consumption, Cognitive Function, and Nobel Laureates. New England Journal of Medicine 2012;367:1562-

Le feuilleton épidémio-statistique publié dans MEDINLUX.