Der buchstabe „P“: klein in der grösse, aber gross im geist

Die Wissenschaft der Daten verstehen

• Kompetenzzentrum für Methodik und Statistik

Dieser Artikel wurde in MedinLux veröffentlicht und ist Teil einer gemeinsamen Anstrengung, statistische und epidemiologische Konzepte den Angehörigen der Gesundheitsberufe in Luxemburg zugänglich zu machen.

Dieser Artikel ist der erste in einer Reihe über statistische Methodikfragen, die Werkzeuge bereitstellt, um wissenschaftliche Artikel besser zu verstehen und zu interpretieren. Das Ziel ist es, ein kritisches Denken zu entwickeln und die bewährten Verfahren beim Lesen wissenschaftlicher Informationen (oder bei der Analyse Ihrer eigenen Daten) zu kennen. In der biomedizinischen Forschung ist es üblich, Ausdrücke wie „statistisch unterschiedlich“ oder „signifikant größer/kleiner“ zu lesen, Tabellen mit einer Spalte zu sehen, in der der Buchstabe „p“ erscheint, oder Diagramme mit Sternen (oder anderen Symbolen) zu finden. All dies bezieht sich auf die gleiche Idee: den p-Wert (probability value auf Englisch). Aber was bedeutet dieser? In diesem Artikel werden wir Ihnen diesen Wert ausführlicher vorstellen.

EIN BEISPIEL AUS DER LITERATUR, UM UNSER ANLIEGEN ZU VERDEUTLICHEN

In einem wissenschaftlichen Artikel aus dem Jahr 2021 untersuchten die Autoren das Geburtsgewicht von Babys in Abhängigkeit vom Tabakkonsum der Mütter (1), wobei sie den Body-Mass-Index (BMI) der Mütter berücksichtigten. Die Daten stammten aus einer deutschen perinatalen Studie und umfassten mehr als 110.000 Schwangerschaften, die zwischen 2010 und 2017 beobachtet wurden. Die Zusammenfassung gab an, dass die Gewichtsunterschiede der Babys zwischen Raucherinnen und Nichtraucherinnen stets statistisch signifikant waren (p < 0.001), unabhängig vom BMI der Mutter.

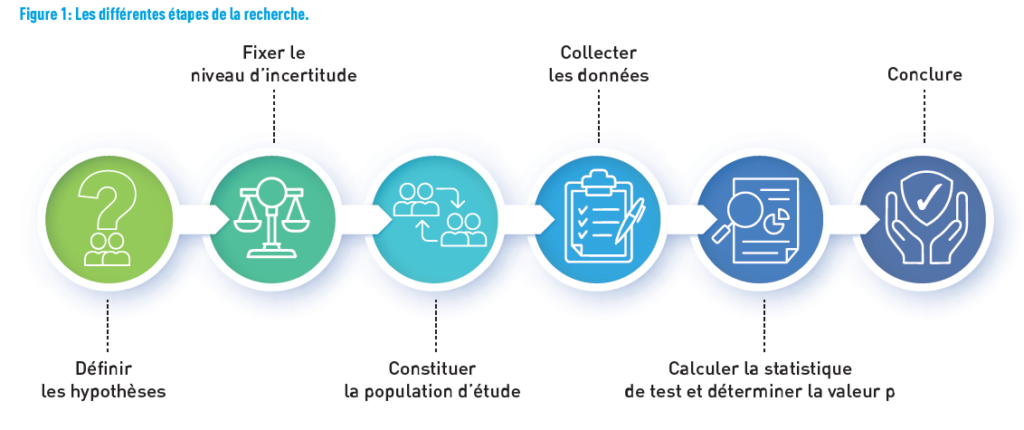
Versetzen wir uns in die Lage des Forschungsteams und stellen uns die Fragen, die sie sich gestellt haben müssen. Das Ziel des Teams war es, die Beziehung zwischen dem Rauchen und dem Geburtsgewicht unter Berücksichtigung des mütterlichen BMI zu analysieren. Abbildung 1 zeigt die verschiedenen Schritte von der Definition der Forschungshypothese bis zu den Schlussfolgerungen.

ZUERST DIE HYPOTHESE DEFINIEREN

In der Forschung zielt der hypothetisch-deduktive Ansatz darauf ab, eine Nullhypothese und eine Alternativhypothese explizit zu definieren. Die Nullhypothese wird formuliert, um widerlegt zu werden. Sie wird als wahr angenommen, solange das Gegenteil nicht bewiesen ist. Im Gegensatz dazu ist die Alternativhypothese diejenige, die bewiesen werden soll. Sie sind disjunkt: Beide Hypothesen können nicht gleichzeitig zutreffen.

In unserem Beispiel lautet die Nullhypothese: „Es gibt keinen Gewichtsunterschied zwischen den Babys von rauchenden oder nichtrauchenden Müttern“, während die Alternativhypothese so formuliert werden kann: „Es gibt einen Unterschied im Geburtsgewicht der Babys zwischen Raucherinnen und Nichtraucherinnen.“

In der Praxis basiert die Entscheidung auf der Nullhypothese, wobei man hofft, die Alternativhypothese zu beweisen. Wissenschaftler verwenden statistische Tests, um zu bestimmen, ob die Nullhypothese wahr oder falsch ist. Wenn sie mit einer gewissen Wahrscheinlichkeit nachweisen können, dass die Nullhypothese falsch ist, wird die Alternativhypothese akzeptiert (2).

FESTLEGUNG DES UNSICHERHEITSNIVEAUS

Sobald die Hypothesen klar formuliert sind, wird die Fehlerwahrscheinlichkeit 1. Artbetrachtet, also das Risiko, das man eingeht, wenn man die Nullhypothese ablehnt (und somit die Alternativhypothese akzeptiert), obwohl sie wahr ist. Dies ist der Fehler erster Art oder α -Fehler, notiert als α. Sie ist je nach Bereich und Zielsetzung der Studie zu bestimmen. Im Allgemeinen wird sie auf 5% festgelegt. Das bedeutet, dass wenn eine Studie z.B. 100 Mal durchgeführt wird (z.B. an verschiedenen Stichproben), die Nullhypothese fünf Mal abgelehnt wird, obwohl sie wahr ist.

BEMERKUNG DER BIOSTATISTIKERIN
Die Wahl des 5%-Werts ist nicht zufällig. Diese Grenze stammt aus einer Normalverteilung (auch Gauss-Verteilung genannt, die berühmte Glockenkurve, ein absolutes Referenzmodell in der Statistik, das die Verteilung vieler biologischer Variablen beschreibt): Wenn Werte mehr als zwei Standardabweichungen von dem Mittelwert entfernt sind (bei einer Normalverteilung mit einem 5%igen Fehler, was einem Schwellenwert von 1.96 entspricht), gelten sie als ungewöhnlich (3). Ein Statistiker kann versuchen, dieses Risiko zu minimieren, indem er zum Beispiel einen Schwellenwert von 1% anstelle von 5% wählt, was jedoch dazu führt, dass es schwieriger wird, die Nullhypothese abzulehnen

Eine weitere zu beachtende Fehlerart: der „false positive“. Beim statistischen Hypothesentest kann es passieren, dass die Nullhypothese akzeptiert wird, obwohl sie falsch ist. Dies nennt man einen Fehler zweiter Art, notiert als β. In unserem Beispiel würde das bedeuten, dass man sagt, die Babys hätten das gleiche Geburtsgewicht, unabhängig davon, ob ihre Mütter rauchen oder nicht (obwohl das nicht der Fall ist). Dieser Fehler wird bei der Berechnung der Teststärke (1-β) verwendet, die die Wahrscheinlichkeit darstellt, die Nullhypothese abzulehnen, wenn sie falsch ist.

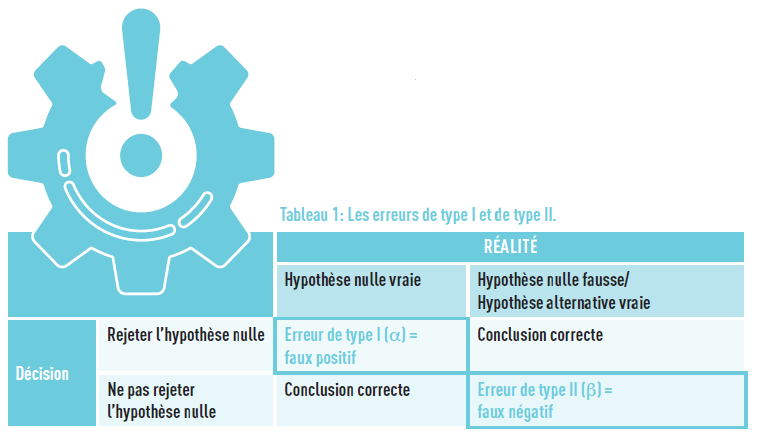
Diese beiden Fehlerarten sind miteinander verknüpft: Wenn der eine verringert wird, erhöht sich der andere und umgekehrt. Tabelle 1 fasst die verschiedenen Situationen zusammen.

ZUSAMMENSTELLUNG DER STUDIENPOPULATION

Bevor eine Studie begonnen wird, ist es wichtig, die Anzahl der einzubeziehenden Teilnehmer zu bestimmen. Warum ist dieser Schritt notwendig? Um zu vermeiden, dass zu viele Patienten rekrutiert werden, was erhebliche Kosten und/oder Zeitaufwand verursachen würde, oder um ethische Probleme zu vermeiden, insbesondere bei interventionellen Studien (Exposition gegenüber potenziell unwirksamen oder gar gefährlichen Behandlungen). Umgekehrt würde eine zu kleine Stichprobengröße nicht ausreichen, um eine ausreichende statistische Power zu erreichen und somit keine eindeutige Schlussfolgerungermöglichen.

Für die Bestimmung dieser Zahl sind mehrere Informationen erforderlich: die erwartete Effektgröße (basierend auf vorhandenen Forschungsergebnissen), die Power, der Fehler 1. Art, die Datenvarianz und das statistische Modell, das in der Analyse verwendet wird. Die Stichprobe muss zudem repräsentativ für die Zielpopulation sein, das heißt, sie sollte wichtige Eigenschaften mit dieser teilen. So repräsentiert die Stichprobe möglichst genau die Merkmale der Zielpopulation, beispielsweise das Geschlechterverhältnis oder das Durchschnittsalter. Ohne diese Voraussetzungen können die Ergebnisse der Studie nicht verallgemeinert werden.

In unserem Beispiel suchten die Autoren nach Daten über die Babys und den Tabakstatus der Mütter.

DATENSAMMLUNG

Nachdem all diese Punkte im Voraus festgelegt wurden, können die Daten gesammelt werden.

In unserem Beispiel nutzten die Forscher eine umfangreiche Datenbank aus der Provinz Schleswig-Holstein, die Teil der German Perinatal Survey (Neugeborenenkollektiv) war und 110.047 einzelne Schwangerschaften zwischen 2010 und 2017 umfasste. Dies ist also eine Registerstudie (wir werden später auf die verschiedenen Studientypen mit ihren Vor- und Nachteilen sowie ihren Einschränkungen eingehen), die eine beträchtliche Stichprobengröße hat (was ein Indikator für die statistische Power ist, siehe Kasten).

Nach Abschluss der Datensammlung können die verschiedenen im Protokoll vorgesehenen Indikatoren berechnet werden, die zur Beantwortung der Forschungsfrage notwendig sind (zum Beispiel der Durchschnitt eines Parameters in den verschiedenen Gruppen, ein Odds Ratio, ein relatives Risiko usw.). Diese verschiedenen Konzepte werden in einem kommenden Artikel behandelt. In unserem Beispiel berechneten die Forscher das durchschnittliche Gewicht der Babys in der Rauchergruppe und das durchschnittliche Gewicht in der Nichtrauchergruppe und verglichen diese beiden Werte, wobei sie den BMI der Mutter während der Schwangerschaft berücksichtigten.

BERECHNUNG DER TESTSTATISTIK UND BESTIMMUNG DES P-WERTES

Die grundlegende Frage, die sich an diesem Punkt stellt, ist, ob der Unterschied in unserem Indikator – dem Geburtsgewicht der Babys in Abhängigkeit vom Rauchstatus der Mutter – auf diesen zurückzuführen ist oder ob es sich um einen Zufallseffekt handelt. Um diese Frage zu beantworten, verwendet man statistische Tests, wie den Test der Mittelwerte oder Mediane, oder den Chi-Quadrat-Test, um nur einige der bekanntesten zu nennen, die diesen berühmten p-Wert liefern.

Ein Statistiker kann Ihnen jedoch immer gute Ratschläge geben, welcher Test für Ihre Forschung am besten geeignet ist. Der p-Wert ist eine Wahrscheinlichkeit und liegt daher zwischen 0 und 100%. Je kleiner der p-Wert ist, desto stärker sind die Beweise gegen die Nullhypothese. Anschließend wird er mit dem zuvor definierten Fehler α verglichen. Wenn der p-Wert kleiner als α ist, ist die Alternativhypothese statistisch signifikant, und die Nullhypothese wird mit einem Risiko von α abgelehnt. Andernfalls wird die Nullhypothese akzeptiert.

BEMERKUNG DER BIOSTATISTIKERIN
Für gute Praktiken wird dringend empfohlen, den p-Wert anzugeben, anstatt einen Stern (oder ein anderes Symbol) in einem Diagramm zu verwenden oder „< 5%“/  „< 0.05“ in einem Text oder einer Tabelle zu schreiben!

In unserem Beispiel war das Geburtsgewicht bei Nichtraucherinnen am höchsten. In allen Gruppen des mütterlichen BMI nahm das Geburtsgewicht signifikant mit der Anzahl der täglich gerauchten Zigaretten ab (p < 0.001). Mit anderen Worten, die Wahrscheinlichkeit, dass der Zufall die beobachteten Unterschiede erklärt, liegt unter 1 zu 1.000 (< 0.1%).

DAS KONFIANZINTERVALL: EIN WEITERER INDIKATOR MIT VIELEN VORTEILEN

Das Konfidenzintervall (KI) liefert mehr Informationen als der p-Wert: Es zeigt die Bandbreite von 95% des gemessenen Effekts (entsprechend einem Risiko von 5%). Dies bedeutet, dass bei 100 Schätzungen des Effekts (unter anderen Bedingungen: unterschiedliche Personen, Regionen, Zeiten) das Ergebnis in 95 von 100 Experimenten in diesem Intervall liegen würde. Darüber hinaus ermöglicht das KI auch Schlussfolgerungen zur statistischen Signifikanz: Im einführenden Beispiel, wenn zum Beispiel das Odds Ratio (das genauer im nächsten Artikel erläutert wird) zwischen der Wahrscheinlichkeit, ein Frühgeborenes zu bekommen oder nicht, je nach Raucherstatus der Mutter berechnet wird. Ist die Zahl 1 nicht im Intervall enthalten ist, bedeutet dies, dass ein statistisch signifikanter Effekt zwischen diesen beiden Variablen mit einem Risiko von 5% vorliegt. Ein weiterer Vorteil des KI ist die Messvariabilität. Wenn es breit ist, ist die Schätzung weniger präzise als bei einem engen KI.

BEMERKUNG DER BIOSTATISTIKERIN: FALSCH POSITIVE ERGEBNISSE UND DIE NOTWENDIGKEIT DER KORREKTUR VON MEHRFACHTESTS

Ein Problem kann auftreten, wenn mehrere Tests an derselben Stichprobe durchgeführt werden. Nehmen wir das Beispiel der Studie über den Einfluss von Tabak auf das Geburtsgewicht von Babys und stellen uns vor, die Autoren möchten auch den Effekt der Einnahme bestimmter Medikamente, körperlicher Aktivität (leicht, moderat oder intensiv), des Verzehrs von Obst und Gemüse, Renovierungsarbeiten im Haus (zur Vorbereitung auf die Ankunft des Babys) oder Stress während der Schwangerschaft testen. Gemäß der Definition werden von 100 Tests mit einem Signifikanzniveau von 5% bei 5 Testsfalsch positive Ergebnisse auftreten.

Um der Inflation des Fehlers erster Art – also fälschlicherweise zu dem Schluss zu kommen, dass es einen Unterschied gibt – bei der Durchführung mehrerer Tests Rechnung zu tragen, gibt es Lösungen wie z.B. die Bonferroni-Korrektur (die bekannteste). Ein Statistiker wird erneut der beste Ansprechpartner sein, um Ihnen eine Lösung für dieses Problem vorzuschlagen!

Bei einem Vergleich mit der Justiz, entspricht der Fehler vom Typ I dem Urteil einer Person als schuldig, obwohl kein Verbrechen begangen wurde, und der Fehler vom Typ II dem Urteil einer Person als unschuldig, obwohl sie das Verbrechen begangen hat.

DAS MULTIPLE TESTPROBLEM

Einige Forscher gehen unabsichtlich rückwärts vor, oft unter Druck, Ergebnisse zu veröffentlichen, anstatt eine Hypothese zu testen. Sie gehen auf die Jagd nach statistischen Assoziationen. Diese Praxis ist unter verschiedenen Namen bekannt: p-hacking, data dredging, data fishing, data snooping oder data butchery. Es kann sich in verschiedenen Formen zeigen: Analysen durchführen, bis Ergebnisse mit einem p-Wert unter einem bestimmten Schwellenwert (normalerweise 0.05) gefunden werden, Änderung der Bewertungskriterien, Verwendung eines eingeschränkten Datensatzes mit einer anderen Population als der ursprünglichen (durch Ausschluss von Teilnehmern oder Auswahl nur einer bestimmten Bevölkerungskategorie), Verwendung von zusätzlichen oder vergessenen Anpassungsvariablen oder nur die Darstellung signifikanter Tests (Publikationsbias). Durch Entfernen nicht signifikanter Tests steigt die Wahrscheinlichkeit, signifikante Ergebnisse zu finden. Die Nichtanwendung von Korrekturen für multiples testen ist eine Möglichkeit, Ergebnisse zu verändern, so dass Ergebnisse rein zufällig signifikant werden können (siehe vorheriger Absatz).

Immer mehr Zeitschriften sind sich dieser Problematik bewusst: Deshalb fordern sie die Veröffentlichung der Daten, um Analysen replizieren und die veröffentlichten Ergebnisse nachvollziehen zu können.

Gute Praxis ist es, im Voraus einen statistischen Analyseplan zu erstellen, der verschiedene Analysen beschreibt sowie die die Hypothesen und die vorgesehenen Lösungen, immer mit der Unterstützung eines Statistikers.

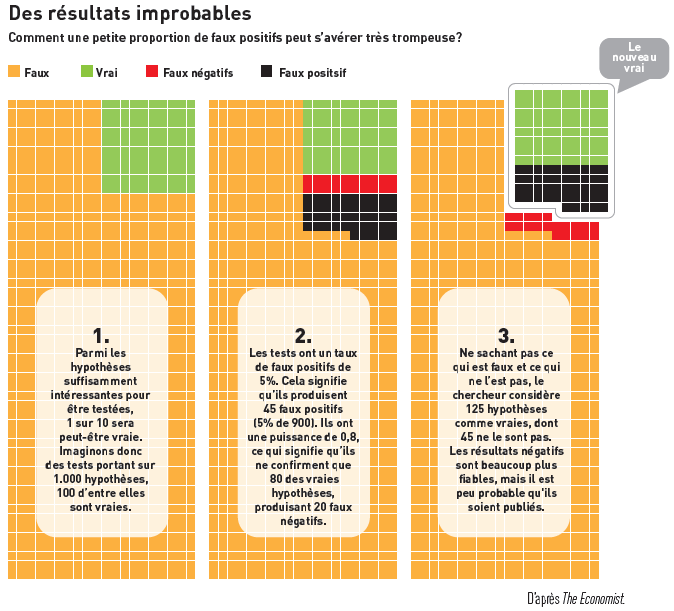
KONTROVERSE ÜBER DEN p-WERT

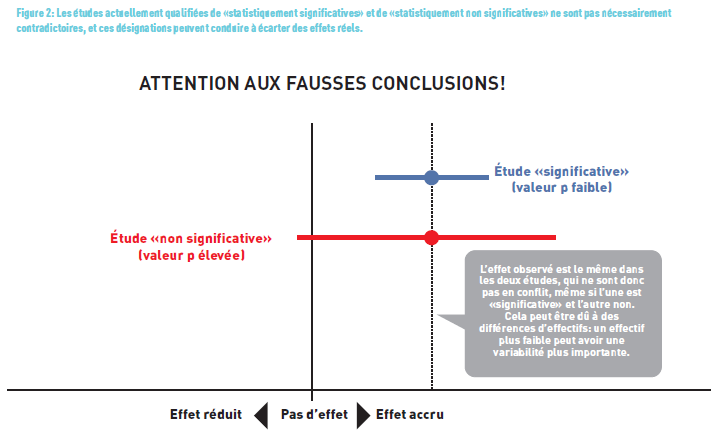
In den letzten Jahren (sogar Jahrzehnten) haben viele Statistiker den p-Wert kritisiert, insbesondere in einem Artikel, der in Nature veröffentlicht wurde (4) (Abbildung 2). In diesem Artikel stellten die Autoren fest, dass 51% der 791 Artikel aus 5 Zeitschriften den p-Wert falsch interpretierten. Sie wünschen sich, dass dieser Indikator nicht mehr dichotomisiert wird in „statistisch signifikant“ / „statistisch nicht signifikant“, um eine Entscheidung zu treffen. Der p-Wert sollte nicht abstrakt beurteilt, sondern in seinem Kontext betrachtet werden, wobei man sich immer bewusst sein sollte, dass die statistische Bedeutung von der klinischen Bedeutung abweichen kann.

TAKE-HOME-NACHRICHTEN

Der p-Wert ist ein Standard in wissenschaftlichen Artikeln, obwohl seine Interpretation fehlerhaft sein kann. Durch Anwendung bestimmter Regeln können jedoch die in diesem Artikel erwähnten Fallstricke vermieden oder sogar bessere Schätzungen durch die Verwendung von Konfidenzintervallen ermöglicht werden. Die Berechnung des p-Wertes ist technisch anspruchsvoll, da sie Kenntnisse und Fähigkeiten erfordert, um den geeigneten statistischen Test zu bestimmen. Oft wird die Signifikanzschwelle auf 5% (0.05) festgelegt, aber sie kann gesenkt werden, um die Wahrscheinlichkeit zu verringern (oder erhöhen, je nach Bedarf), dass die beobachteten Unterschiede zufällig sind. Darüber hinaus sollte die Interpretation nicht binär (signifikant / nicht signifikant) als richtig oder falsch betrachtet werden, sondern es ist wichtig, die gesamte Studie und insbesondere den gemessenen Effekt zu berücksichtigen!

Zögern Sie nicht, uns Ihre Fragen zu epidemiologischen oder statistischen Themen zuzusenden. Wir werden darauf zeitnahantworten.

«NICHT SIGNIFIKANT» BEDEUTET NICHT „KEIN EFFEKT“!

Eine Studie kann keinen Effekt zeigen aufgrund einer unzureichenden Anzahl von Teilnehmern/Stichproben (was die Teststärke schwächt, d.h. ihre Fähigkeit, die Nullhypothese abzulehnen, obwohl diese falsch ist), oder sogar aufgrund eines Fehlers 1. Art (falsch-positiv). Es ist wichtig, statistische Signifikanz zu unterscheiden – die mit einem gewissen Grad an Unsicherheit die Realität eines Unterschieds bestätigt – von der klinischen Relevanz dieses Unterschieds. Um diesen Grundsatz zu formulieren, ist die Größe (oder Stärke) des Effekts zu berücksichtigen, zum Beispiel durch eine bedeutende relative Risikoreduktion. Wir werden später auf dieses grundlegende Konzept zurückkommen.

In ähnlicher Weise lässt ein statistisch signifikantes Ergebnis keine Rückschlüsse auf eine mögliche Kausalität zu. In einer Arbeit, die im New England Journal of Medicine (5) veröffentlicht wurde, fanden die Autoren eine hochsignifikante Korrelation (r = 0.791 und p < 0.0001) zwischen dem Konsum von Schokolade und der Entwicklung kognitiver Funktionen, gemessen an der Anzahl der Nobelpreise pro Land. Sie schlossen humorvoll, dass noch zu bestimmen bleibt, ob der Schokoladenkonsum der zugrunde liegende Mechanismus der beobachteten Assoziation mit der Verbesserung kognitiver Funktionen ist. Wir werden später sehen, dass zur Feststellung eines Kausalzusammenhangs zwischen einem Faktor und einem Ereignis eine Reihe von Kriterien (sogenannte „Bradford-Hill-Kriterien“) erfüllt sein müssen.

Zusammenfassung statistischer konzepte durch die biostatistikerin

• Das Ziel eines statistischen Tests ist es, eine Nullhypothese (H0) zu überprüfen.
• Die Nullhypothese betrifft einen Parameter der Population.
• Die Nullhypothese ist diejenige, die wir ablehnen möchten. Sie drückt oft das Fehlen eines Effekts aus. Zum Beispiel: Die Wirkung von Behandlung A ist gleich der Wirkung von Behandlung B.
• Die Alternativhypothese (H1) ist diejenige, die wir beweisen möchten. Zum Beispiel: Die Wirkung von Behandlung A ist unterschiedlich zur Wirkung von Behandlung B.
• Es gibt 2 Arten von Fehlern:
  • Fehler 1. Art: Ablehnung von H0, obwohl sie wahr ist (falsch-positiv). Die Wahrscheinlichkeit dieses Fehlers beträgt α.
  • Fehler 2. Art: Nicht-Ablehnung von H0, obwohl sie falsch ist, d.h. wenn H1 wahr ist (falsch-negativ). Die Wahrscheinlichkeit dieses Fehlers beträgt β.
• Die Teststärke (Power) eines statistischen Tests entspricht 1-β. Dies ist die Wahrscheinlichkeit, H0 abzulehnen, wenn sie falsch ist (und daher H1 wahr ist).
• Statistische Tests bestimmen den p-Wert, der eine Wahrscheinlichkeit ist (also zwischen 0 und 100%).
• Je kleiner der p-Wert ist, desto stärker sind die Beweise gegen die Nullhypothese H0. Wenn der p-Wert kleiner als der Fehler α ist, sind die Ergebnisse statistisch signifikant. Andernfalls wird die Nullhypothese akzeptiert.

References

1. Günther V, Alkatout I, Vollmer C, et al. Impact of nicotine and maternal BMI on fetal birth weight. BMC Pregnancy Childbirth 2021;21:127. https://doi.org/10.1186/s12884-021-03593-z
2. www.eupati.eu
3. Cowles, M., & Davis, C. (1992). On the origins of the .05 level of statistical significance. In A. E. Kazdin (Ed.), Methodological issues & strategies in clinical research (pp. 285–294). American Psychological Association. https://doi.org/10.1037/10109-026
4. Amrhein, Valentin, Sander Greenland, and Blake McShane. 2019. “Scientists Rise up against Statistical Significance.” Nature (London) 567 (7748): 305–7. https://doi.org/10.1038/d41586-019-00857-9.
5. Messerli FH. Chocolate Consumption, Cognitive Function, and Nobel Laureates. New England Journal of Medicine 2012;367:1562-

Die in MEDINLUX veröffentlichten epidemiostatistischen Reihen.